Analyse verschiedener Kreuzungssituationen im Straßenverkehr

W-Seminar

Lukas Eisenhauer

### Problematik der Verkehrskreuzung Notwendigkeit des schnellen Transports Ziele: - Keine verstopften Kreuzungen - kurze Reisedauer

### Wie Erkentnisse sammeln? - Ideal: Experiment - Problem: hohe Kosten: 30000€ Bei 10 Menschen und 12 € Stundenlohn. - Alternative: Simulation erstellen - Zusätzlich: Kontrolle aller Variablen möglich

### Plan 1. Physikalische Hintergründe zur Simulation von Autos in einem Verkehrssystem 1. Simulation verschiedener Kreuzungen 1. Analyse der erhobenen Daten 1. Einblicke in die Einflüsse verschiedener Variablen

### Absichtliche Kräfte | Antriebskraft $F_{Motor}$ | Bremskraft $F_{Bremse}$ | | ------------------------- | ----------------------- | | Annahme: konstante Motorleistung | kein intrinsisches Limit (bessere Bremsen leicht umsetzbar) | | $F_{Motor} \leq \frac{P}{v}, P = 2500$W | |

### Widerstandskräfte | Rollwiderstand | Luftwiderstand | | --- | --- | | Deformation der Räder | Kollision mit Luftmolekülen | | $F_{Roll} = F_{g} * c_{R}$ | $F_{Luft} = \frac{1}{2} * c_{W} * \rho * A * v^{2} $ | $c_{R} = 0,02$ | $c_{W} = 0,4 $ |

### Haftreibung - maximale Kraft, bevor ein Körper „rutscht“ - Haftverlust soll vermieden werden $$ F_{Haft} = F_{g} * \mu, \mu = 0,9 * \frac{\sqrt{2}}{2} $$ $$ F_{Zentripetal} = \frac{m * v^{2}}{r} $$ $$ F_{Haft} \leq F_{Zentripetal} ⇔ v \leq \sqrt{\mu * g * r} $$

### Entscheidung: Bremsen oder beschleunigen? - schreiben einer Funktion $v_{Brems}(s)$ - bremsen, wenn $v_{Brems}(d_{Vordermann} - v * 1,8\mathrm{s}) \leq v_{Vordermann}$ - bremsen, wenn $v_{Brems}(s) \leq v_{Max}(s) $ - Ampeln - Vorfahrtsregeln (Kreisverkehr)

### Summe aller Kräte $$ F_{gesamt} = F_{Motor} - (F_{Bremse} + F_{Roll} + F_{Luft}) $$ $$ a = \frac{dv}{dt}, v = \int \frac{F}{m} * dt, v = \frac{ds}{dt}, s = \int a * dt $$ $$ v(t + \Delta t) = \sqrt{\frac{a_{konst}}{B}} * tan(-\Delta t * \sqrt{a_{konst}*B} + $$ $$ tan^{-1}(v_{0} * \sqrt{\frac{B}{a_{konst}}})) $$

Alle Gesetzmäßigkeiten zusammen

### Messerhebungsverfahren - $15$ Minuten lange Simulationen - Erwartungswert der Reisezeit $E(t_{Reise})$ - $P_{keinPlatz}$: welcher Anteil an Autos kann nicht erzeugt werden? - Erkenntnis: $P_{keinPlatz}(f) = m * f + 1$

| Streuung der Messwerte | Ermittlung des maximalen Durchsatzes | | --- | --- | |  |  |

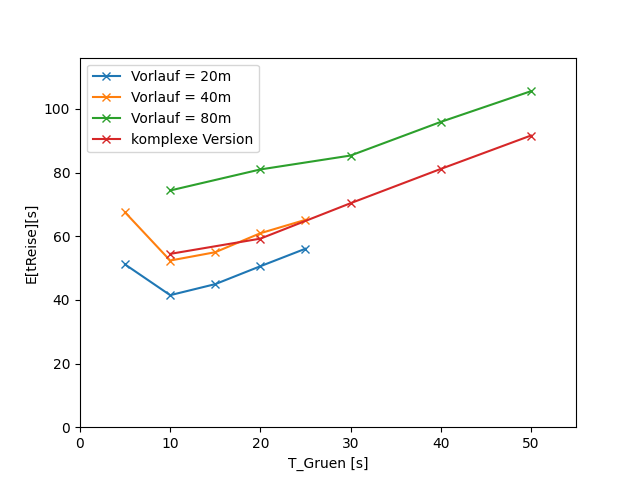
### Eine einzelne Ampel Untersuchte Variablen: - Grünanteil - Periodendauer - Vorlauf vor der Ampel 

### Eine einzelne Ampel | Verschiedene Grünanteile | | --- | |  |

### Eine einzelne Ampel | Verschiedene Periodendauern | Verschiedene Vorlaufdistanzen | | --- | --- | |  |  |

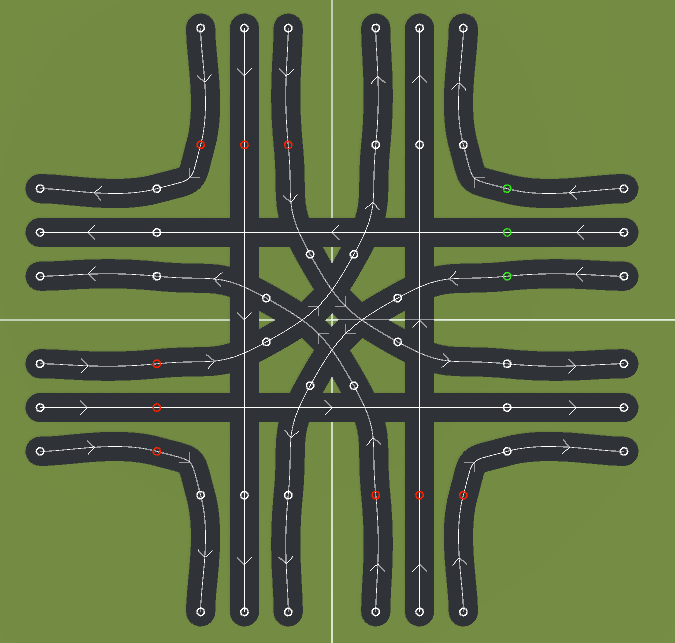
Die Vier-Wege-Kreuzung

Einfache Kreuzung	Komplexe Kreuzung

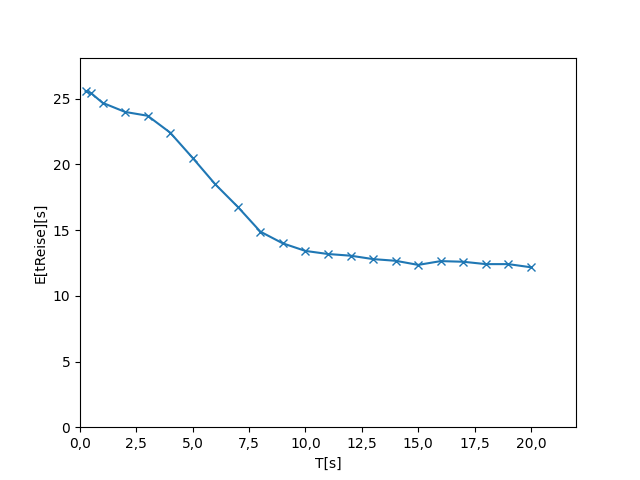
### Die Vier-Wege-Kreuzung | maximale Frequenz | Reisezeit | | --- | --- | |  |  |

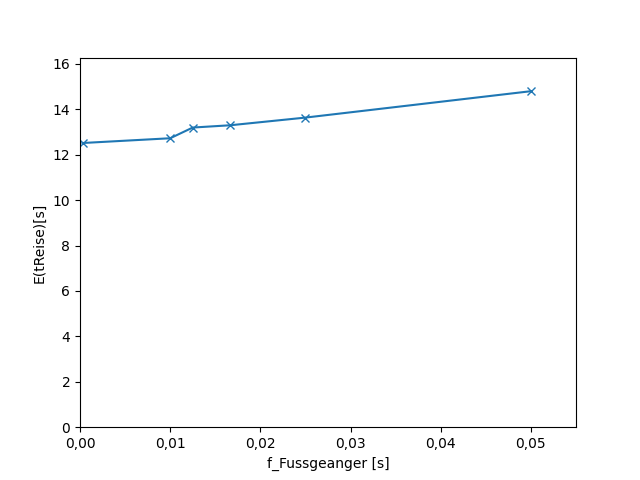
Der Kreisverkehr

Untersuchter Parameter: Einfluss von Fußgängern

### Der Kreisverkehr | maximale Frequenz | Reisezeit | | --- | --- | |  |  |

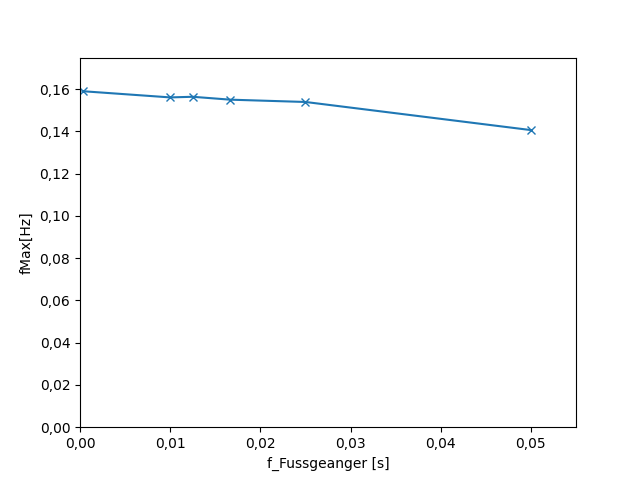Der Kreisverkehr

Reisezeit	Video

### Probleme des Kreisverkehrs - Gefahren für Fußgänger - Platzbedarf 

### Zusammenführung aller Daten 

### Zentrale Erkentnisse - Kreuzungen müssen an vorhandene Nachfrage angepasst werden - Kreisverkehr einer einfachen Kreuzung verkehrstechnisch überlegen - Probleme beim Kreisverkehr vorhanden

### Ausblick - Straßen mit Höhenunterschieden - Varianz im Fahrverhalten - Varianz in den Spezifikationen der Autos - Reale Bestätigung der Messwerte - verbesserte Kollisions - und Vorfahrtsbestimmung